62 replies to this topic

[maciej1986]

merckx a jaka to różnica??

[merckx]

merckx a jaka to różnica??

kolejność wykonywania działań :roll:

[nikodem]

hmm a można jeszcze tak ale to będzie wartość przybliżona i w stopniach
potrzebny nam jest do tego przyrządzenie mierzące dystans(długość) i wys nad poziomem morza i tablica wartości sinusów
b-dystans w metrach
a-przewyższenie w metrach
a/b=sin
sinus odczytujemy,odczytujemy jest! cudowny przybliżony wynik w stopniach
Oto przykład
podjazd 5km
przewyższenie 250m
250/5000=sin
0.05=sin
czyli o 3 stopnie
a tak się liczy procentowo
http://sport.onet.pl...12,0,forum.html
jeden z komentarzy
http://sport.onet.pl...12,0,forum.html

[piter]

merckx a jaka to różnica??

kolejność wykonywania działań :roll:

Czyli, że mnożenie nie ma jakieś cudowne pierwszeństwo nad dzieleniem i stąd potrzebujemy tych nawiasów?

W ogóle to strasznie fajny temat.

[Rowerex]

Trygonometria nie jest w ogóle potrzebna: sin(x)=tg(x)=x dla małych kątów, czyli 1 stopień w procentach to 100*pi/180=1,75%

A tu tabelka porównująca trzy metody, sinusową, tangensową i zwykłe mnożenie kąta razy 1,75



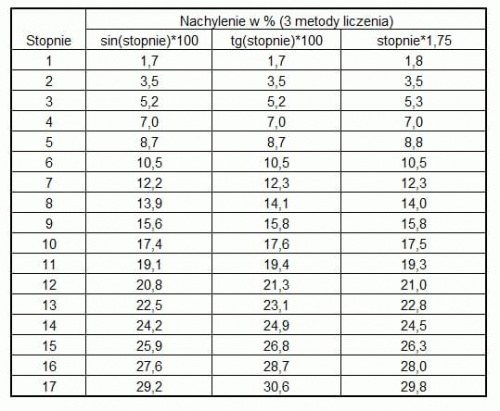
Jak widać wszystkie trzy metody aż do 30% nachylenia dają bardzo zbliżone wyniki, więc można je uznać za równoważne.

[comet1]

Rowerex - czyżby???
jeśli 90° - 100%
to 1° - 1.11111111111%
lub 1% - 0.9°

czyli nachylenie np. 30° to około 33%
a nachylenie 30% to 27°

[Rowerex]

Jeszcze raz:)

45° to 100% nachylenia - wg klasycznej miary tangensowej, czyli
[(przewyższenie)/(odległość w poziomie)]*100% Uwaga: odległość mierzona jest w poziomie, a nie pod górę!

1° to 1,75% - tu zarówno miara tangensowa jak i sinusowa, [(przewyższenie)/(odległość pod górę]*100%, dają pomijalne różnice w wynikach:

sin(1°)*100% = 1,745240...... %
tg(1°)*100% = 1,745506..... %

Do ok 20° nachylenia można założyc liniowość funkcji sinus i tangens, powyzej 20° zaczynają się znaczne nieliniowości i różnice między funkcjami i wyniki się rozjeżdżają

sin(20°)*100% = 34,20201....
tg(20°)*100% = 36,39702...

Różnice nadal nie są takie duże, a przecież podjazdu szoswego 34-36% raczej nie sposób znaleźć, nie mówiac o próbie podjechania tego szosówką...

Obrazek który wkleiłem to obliczenia w excelu - wniosek z nich taki, ze wystarczy mieć coś co mierzy nachylenie w stopniach i pomnożyć wskazane stopnie razy 1,75% aby otrzymac nachylenie procentowe - błąd będzie pomijalny na wszystkich podjeżdzalnych podjazdach na świecie.

[comet1]

a kto to założył, że 45° to 100% ?
ja byłem nauczony iż 90° to 100%

ale i tak przy założeniu 45° - 100%
1° daje 2.222222222222222222222% !

[maciej1986]

A ja zaproponuje sposob mierzenia nachylenia za pomocą poziomnicy. Najwygodniej jest z 1metrową, opierasz o jezdnię podnosisz jedna strona aby ustawić ja w poziomie i mierzysz ile cm nad podłożem znajduje sie poziomnica, otrzymujesz gotowy wynik w procentach. Pozdrowienia z 1OSK w Grudziadzu!!

[ Dodano: 2008-10-14, 11:56 ]
To kolego zle zostales nauczony. Juz wyjaśniam. Biorąc pod uwage trójkąt prostokątny którego przyprostokatne sa równe 1m, to bedzie no obrazował przekrój trasy o nachyleniu 100%. Jedna przyprostokatna jest przesunięciem poziomym, druga pionowym. A przeciwprostokatna bedzie trasa pokonana przez np kolarza.

[Miguel]

Ale wtedy nie wyjdzie Ci średnie nachylenie całego podjazdu. Nie wiem po co Wam te tangensy itp. najprostszy sposób to podzielić różnicę wzniesień przez długość podjazdu w metrach i pomnożyć przez 100%. Proste!

[Rowerex]

Tu jest wszystko:

http://pl.wikipedia....e_poziome_trasy

[maciej1986]

Po to im te tangensy zeby bylo wyliczone dokladniej!! Przy podjeździe 100% i przewyższeniu 1m musisz pokonać ok 1.4m drogi, a nie 1m. Oczywiscie im mniejsze nachylenie tym bedzie mniejsza roznica.

[Rowerex]

najprostszy sposób to podzielić różnicę wzniesień przez długość podjazdu w metrach i pomnożyć przez 100%. Proste!

To jest właśnie sinus Niestety jest to też zbyt proste, ponieważ określa nachylenie średnie całości, nie uwzględniając krótkich ale ostrych nachyleń lokalnych, które mogą znacznie przewyższać średnią.

Taką metodę wykorzystują liczniki z altimetrem, mierzące różnicę wysokości na podstawie zmian ciśnienia i dzielące ją przez przebytą drogę, aby otrzymać nachylenie. Idealem to nie jest, bo nie działa gdy się stoi, dodatkowo trzeba przejechać przynajmniej kilkadziesiąt metrów, jak nie więcej, by otrzymać jako taki wynik.

[Rebe]

Większość godnych uwagi podjazdów znajdziemy w " baza podjazdów szosowych" .
Bardzo ładnie zrobione ,z przyzwoitym opisem , kilku godnych uwago podjazdów brakuje ,ale nic nie jest doskonałe .
Co do wyliczeń i zabaw matematyką to chyba łatwiej znaleść każdemu z nas licznik z wysokościomierzem (GPS) niż przyrząd z pomiarem mocy ,pomijając cenę i dostępnośc tego typu urządzeń .

[merckx]

merckx a jaka to różnica??

kolejność wykonywania działań :roll:

Czyli, że mnożenie nie ma jakieś cudowne pierwszeństwo nad dzieleniem i stąd potrzebujemy tych nawiasów?

Nie, chodzi o to że wynik z dzielenia należy pomnożyć przez 100, nie ma tu żadnej filozofii.

[big75]

Fajne, brawo !!!

( Jest jakaś opcja kasowania albo cofnięcia wstawionych punktów czy trzeba odświeżyć stronę żeby sprawdzić następny podjazd----edit:już wiem jak to zrobić)


Jednak nie takie super jak mi się wydawało bo odległość niestety liczona w linii prostej-samolotowej .Ale i tak brawo.